The Sieve of Eratosthenes
Apparently, Eratosthenes was a cool guy. Who was he? He was a Greek Mathematician. What makes him so cool? He gave an algorithm years ago and it is one of the most known algorithms used today in programming.
I found this technique “cool” for a variety of reasons:
- It is really simple (to understand and to recreate).
- The fact that simple logic actually works.
I learnt about this when I stumbled upon (yet) another question from the previously mentioned book.
This question asked to create a simple program which generated the prime numbers up to a given number entered by the user. As a hint, the question asked to research about the ‘Sieve of Eratosthenes’ and hence, here I am.
So what is the ‘Sieve of Eratosthenes’?
Imagine a sieve. You have small rocks in the water and you want to separate the water from the rocks. What do you do? You take a sieve, pour the water (with the rocks in it) from one side, and the clear water comes out from the other. Now you have separated the rocks and the water and can use each for whatever purpose you want to.
Now imagine the water to be all the natural numbers and imagine the rocks to be the prime numbers. We pour in the natural numbers (“water”) from one side and the prime numbers (“rocks”) are left over on the sieve. This sieve is called the ‘Sieve of Eratosthenes’.
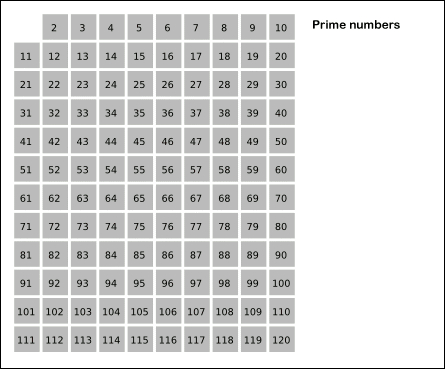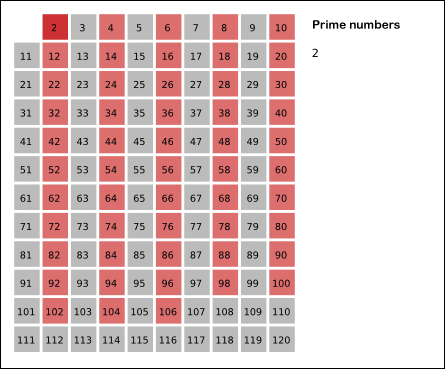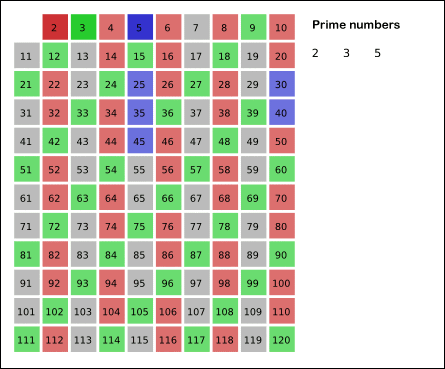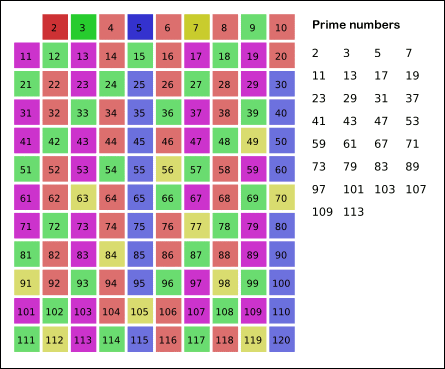
So what it does, basically, is preserves all the prime numbers and eliminates all the natural numbers.
In the problem that I had to solve, this algorithm was applied pretty much straightforwardly, but I believe that it can be used for other useful purposes as well.
What I did to find the prime numbers up to a given number was simple enough:
- I took the input from the user of the value up to which I have to generate the prime numbers and read this value into n.
- I created a boolean vector of size n+1 and initialised all indice to true.
- I first set the values of vector indice 0 an 1 to false. I then wrote a loop which varied the value of an integer i from ‘2’ to ‘n’ i.e., the range of the loop was [2,n].
- Then I used the if construct to check whether the value of vector index i (e.g., if vector was called primes, primes[i]) was true. If it was, the following code would run.
- Then I created a nested loop wherein an integer j was initialised to 0 and the condition was set for (i2 + i*j) to be less than n. This loop set the value of the vector index (i2 + i*j) to false.
- I exited both the loops and finally created a loop which printed the index number of all the vector values set to true.
The only confusing part of this program must be the second loop in the main program.
The body of the loop, that is, primes[i2 + i*j] = false; and the condition (i2 + i*j) < n.
Now, this is the main part of how the sieve works.
What it does is, it eliminates all possible multiples of the index numbers in the vector whose values are set to true and continues this until the multiple of the number becomes greater than the limit itself (n).
You must be wondering, where did i2 + i*j come from? More importantly, why did we square the number (i) before moving on to add the multiples of the number to the square?
The reason is simple: The smallest multiple of a prime number which is not a multiple of it’s preceding prime numbers is the product of the number with itself.
Phew. That was one awesome program. More importantly, it taught me how simple logic can be used in complex applications. This is not only true for programs and applications, but also useful in life.
If you’re ever going through a tough time or have a big problem at hand, remember not to think very hard, but apply simple logic to solve the problems.
Actually, when we think about it, isn’t life like a program itself? Feel free to express your views through comments down below.
A/N: Please excuse me for using ‘rocks’ instead of ‘stones’ in the example above. Stones are small, and rocks are big. There are no ‘small rocks’. The word ‘rock’ just sounded better.